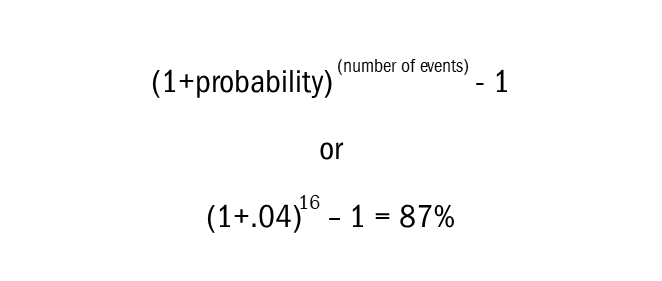For most of us, it’s been a long time since we were in a math class and if we ever learned anything about probability we forgot it all once the final exam was turned in to the teacher. In an age of smartphones and endless apps, thinking about probability just doesn’t seem like it deserves much attention but knowing a small amount could actually help you make better decisions and avoid some pitfalls in business and in life.
The earliest exposure we get to probability is likely to be rolling a 6-sided die while playing a board game with friends or family. The potential outcomes are very clear: a value of 1, 2, 3, 4, 5, or 6 are possible. That’s it. No chance of negative numbers or anything higher than 6. The simple probability here of rolling any specific number is one divided by the number of possible outcomes or 1/6 which is the same as 17% (rounded up for simplicity). For most situations in life, the potential outcomes aren’t nearly this clear and we’re forced to look at past events that were similar and evaluate the outcomes.
A lot could be written about probability but my hope is to share a few instances that are often misunderstood. Because we have an enormous amount of data on sports, let’s start there.
In 2018, the average probability of success for a field goal kick in the NFL was 80%. That’s a very high percentage considering the many different factors involved (successful passes happen 65% of the time). A field goal is not a “sure thing” but it is often treated as if it were by fans and coaches alike.
And…here comes the math!
There are 16 regular season games in the NFL and an average of 2 field goal kicks per game, per team, for 32 kicks total. With a probability of success of 80%, the probability of failure is clearly 20% or (1 – probability of success). What about two failures in a row? To determine the probability of two successive events occurring, multiply the probabilities together. In this case, the probability of two failures in a row is 20% * 20% = 4%. Simple, right?
To further complicate things, consider if two failures in a row might happen at least once during the entire season. There are an average of 32 field goal kicks in a season for a single team so, for this exercise, we’ll assume two kicks in each game. Let’s look at the probability for two kicks to fail in a row. The math for the probability of that failure at least once during the season is:
A probability of 87% is high, even above the probability of a field goal percentage we discussed earlier. Most observers would see two failed field goal kicks in a row and deduce that the kicker was in a slump or he had lost his edge or some other characterization. A coach might even decide not to use his kicker in the next available play when the truth of the probability is that such an occurrence was very likely to occur sometime during the season. High probability events can and due fail to occur. When they fail to occur successively our human nature can cause us to draw flawed conclusions. Takeaway: A small number of occurrences tells us little about chances of success and failure.
How did the “sure thing” turn into what looks like a “sure failure”? The number of occurrences increased. The probability of a low probability event occurring at least once increases dramatically as the number of events increases. The probability of rolling a six on a 6-sided die that we discussed earlier is 17%. If there are two dice, rolling double sixes (or any double number) is 17% X 17% = 3%. This is similar to the two successive missed field goal kicks. Now, if you roll the dice 20 times, the chance of rolling a double-six at least once rises to 77%.
As a final example consider a low probability event that many people see often: car accidents. In 2017, there were 6.4 million car accidents in the U.S., according to the Department of Transportation. In the same period, there were roughly 220.4 billion trips taken in cars. If we look at those numbers alone, the probability of being in a car accident on any single trip is very small (about 0.0029%). However, every trip you take is a new event and as the number of trips increases, the almost impossible becomes possible. If you take three trips per day in your car, the probability of you being in one accident during the year is 3.2%. We won’t dig into the data here but we note, for your safety, that the Automobile Association of America (AAA) commissioned a study in 2017 that showed talking on a cell phone while driving at least doubles the chance of the driver being in an accident. If we double the accident probability to 6.4% per year for frequent cell phone users and crunch still more numbers, we can see that the chance of such a driver being in a car accident at least once in an 11-year period is 100%. Takeaway: A low probability outcome becomes much more probable as the number of events where that outcome could occur increase.
The world of investing is far removed from a simple roll of a 6-sided die but there are vast amounts of data that can be reviewed. This includes information on individual stocks, industries, changes in interest rates by the Federal Reserve, the impact of a CEO’s shoe size on stock performance. Ok, I made up that last one.
Bottom line: There is a sea of data. At MONTAG, we take the imperfect probabilities we see into account as we make decisions, being careful to remember that the future will rarely look exactly like the past data that we incorporate in our decision process. Probability assessment like the examples given here do not guarantee success but they can help to reduce the emotion in decision making and anchor the process to something we can measure. We think this is a very wise step.
